子供の看病で1日つぶれてしまいました。
私自身も風邪がうつり、喘息で息苦しい日々です。
三角関数がレーザープリンタの技術とどう関わってくるのか、まずは中学レベルの基礎の基礎でみてみました。
そこで出てきた式
x=L×tanθ
をもとに、もう少し調べてみました。
この式は、x(感光体、もしくは光束測定位置)の画像幅は、L(ミラーから感光体までの距離)にtanθをかけることで求められる、ということを表しています。
このtanθというのは、三角関数の表などから数値を参照してもわかるように、角度の変化と比例していないんですね。
| θ | tanθ | 増え方 |
|---|---|---|
| 0° → 5° | 0 → 0.087 | 0.087 増える |
| 5° → 10° | 0.087 → 0.176 | 0.089 増える |
| 10° → 15° | 0.176 → 0.268 | 0.092 増える |
| 15° → 20° | 0.268 → 0.364 | 0.096 増える |
| 20° → 25° | 0.364 → 0.466 | 0.102 増える |
| 25° → 30° | 0.466 → 0.577 | 0.111 増える |
グラフにすると、角度が小さいうちはほぼ直線だけれど、角度が90度に近くになるにつれ、曲線状に上昇していく。
こういうのを「非線形」というらしいです。
比例関係でグラフが直線状のものを「線形」、比例で直線でないものを「非線形」。tanθは非線形の動きをします。
これが何を意味するかというと、レーザー光の速さ(横向き照射速度)が一定ではないということです。
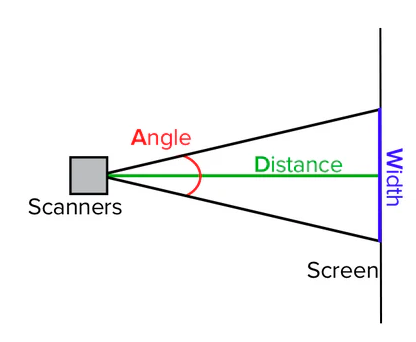
前回参照したこちらの画像をもう一度みてみると、この図の照射分(三角形)が印刷する1ラインに相当するとします。
つまり、三角形の底辺の端から端までを、ミラーに反射されたレーザー光が感光体に照射していきます。これで1ライン。ポリゴンミラー(6面だったり、10面だったり)の1面分が1ライン分に相当します。
ここでtanθが非線形の動きをするので、レーザー光が感光体の端に当たるときは、感光体までの距離L(Distance)となす角度(Angle)が大きいのでtanθも大きいですが、中央付近ではその角度が小さくなるのでtanθは小さくなります。
ここで速度は、速度v=位置の変化(dx)÷時間の変化(dt) で表せます。
位置が時間に対して均等に増えれば「速度一定」だとわかります。
位置の変化が時間の中でバラつくと「速度が変わる」ことがわかります。
図でx(Width)が、同じ時間でも少ししか動かないときは、速さは遅い。逆に同じ時間で大きく動くときは速い、といえます。
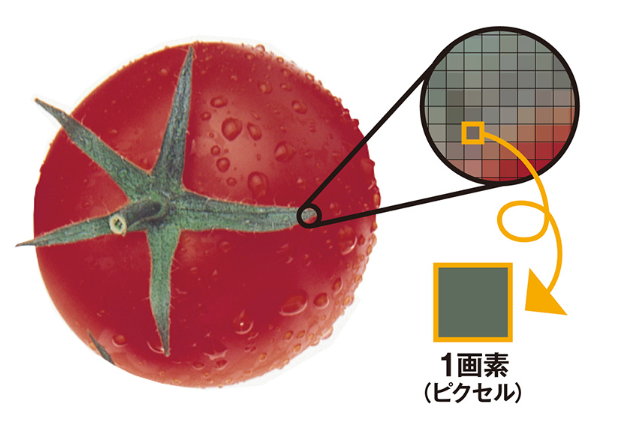
レーザープリンタは、1ラインで数千~数万の画素があります。
この1ラインの中で、毎ドットの間隔が同じでないといけません。
なので、端と中央で速度が違うと、この画素の間隔がずれてしまい、画質劣化につながってしまうのです。
これを補正するためにf-θレンズというものがあります。
これについてはまた今度。
レーザーの横移動速度が一定でないことがわかりました。
ではそのレーザー光を反射させているポリゴンミラーの回転速度はというと、これはポリゴンモータで高速回転しているので、理論上は一定速度で回っています(揺れや温湿度などの外的要因で多少ムラは出る)。
これを数式で表すと、角速度ω=θ÷t。
変形すると、θ=ω×t。
時間に比例して角度が増えることがわかります。こちらはグラフにすると線形グラフになります。
では、時間 t のときのレーザーの横方向の位置 x(t) はどうなるでしょうか。冒頭で触れた三角関数の関係を当てはめると、
x(t)=L×tan(ωt)
となります。
ポリゴンミラーは一定角速度で回っているため、角度の変化は等間隔です。
しかし、レーザーが感光体ドラムに向かう光路は斜めであり、横方向の位置は tan(角度) で決まります。
そのため、ミラーがどれだけ正確に一定速度で回転していても、レーザーの横方向の動きはどうしても非線形になる、というわけです。
ここが補正しないといけない部分(基礎の基礎)なのです。








コメント