しばらく仕事と家族の体調不良に振り回されておりました。
こんな調子では翻訳の実務時間がとれません。安定的に稼働時間をとるために調整できるところはあるか。
本調子に戻った今日から模索します。
「圧力・浮力」について物理で学びました。ビデオは36まで終了。
浮力、「浮く」ことについて考えてみました。
レーザープリンターにおいて、浮力はどこにかかっているか?と考え、調べていると、「浮遊トナー」というワードにあたりました。
「浮遊トナー」または「トナー粒子の飛散」が増加すると、プリンター内部の部品汚れやメンテナンスコストの増大を引き起こす問題があるらしい。
今回は「トナーが浮く(舞う)のはなぜ?」について調べたことをまとめます。
トナーとは
トナー(英:toner)は、レーザープリンター及び複写機で使用される、帯電性を持ったプラスチック粒子に黒鉛・顔料などの色粒子を付着させたミクロサイズの粒から成る粉である。静電気を利用して紙にトナーを転写させ、熱によって定着させることで印刷する。
カラー印刷の場合、通常シアン、マゼンタ、黄色、黒の4色が用意される。英語で「tone」とは色調のことであり、それから由来する。(Wikipediaより)
トナーとは、プリンターや複写機で使われる微細な粉末です。
その大きさは、通常5~8μmです。(1μm=1000分の1mm)
空気中のホコリは粗大粒子といって、大きさが約10μm~100μmなので、それよりも小さいことがわかります。
主成分は以下の通り。
- 樹脂
- 顔料
- ワックス
- 帯電制御材
- 添加剤
トナーに使用する樹脂は、基本的には熱可塑性樹脂であれば使用できますが、トナーに求められる様々な要件を満たすものとなるとかなり限定され、現在では、スチレンアクリル系樹脂、ポリエステル系樹脂が市場の90%以上を占めています。
これらの樹脂の密度がおおよそ1.0~1.3g/㎤です。
対して空気の密度はわずか0.001293g/㎤なので、空気に比べてトナー粒子は圧倒的に重いことがわかります。
本来であれば、重い粒子は重力で下に落ちるはずです。
しかし実際には、トナーのような微細な粒子は空中を舞い上がったり、装置の中で飛散したりします。
それはなぜなのでしょうか?
まずはトナーに働く重力と浮力から整理していきます。
トナーの重力と浮力
「物理基礎」で学んだ浮力の公式は、
Fb=ρgV
です。
これは「物体が押しのけた流体の重さ」と同じ浮力が働くという、「アルキメデスの原理」を表しています。
※アルキメデスの原理
「 流体中の物体は、その物体が押しのけている流体の「重さ」(質量が及ぼす重力)
と同じ大きさの浮力を受ける 」
浮力のρは、物体自身の密度ではなくて、押しのけた相手の密度です。この場合は空気の密度になります。
モデルとなるトナーの条件を以下の通りと仮定します。
・直径:8 μm → 8×10⁻⁶ m
・半径:4×10⁻⁶ m
・トナー密度:おおよそ1200 kg/m³
・空気の密度:1.2 kg/m³
・重力加速度:g ≒ 9.8 m/s²
粒子は球だと仮定すると、
・体積 V :4/3πr3
トナーの重力
重力を以下に当てはめて計算してみます。
Fg=mg=ρ(トナー)Vg
Fg=1200 × 2.68×10-16 × 9.8 ≒ 3.2 × 10⁻¹² N
トナーの浮力
浮力を以下に当てはめて計算してみます。
Fb=ρ(空気)gV
Fb=1.2 × 9.8 × 2.68×10-16
同じ体積 V に対して、空気の密度はトナーの 1/1000 なので、
Fb ≒ 3.2 × 10⁻¹⁵ N
つまり、浮力は重力の 約 0.1%に過ぎず、
「重さ」だけを見れば、トナーに対する浮力はかなり小さいことがわかりました。
なぜトナーは舞うのか?
トナーが浮く(舞う)主な原因は浮力ではありませんでした。
(トナーの浮力は、ほんのわずかに押し上げている程度)
トナーの落下や舞い上がりを決めているのは、ガリレオの落下実験でも触れた「空気抵抗」というもう一つの大きな力が関係しています。
ここから先は、その空気抵抗が「粒子の大きさによってどう変わるか」を見ていきます。
空気抵抗は「粒子の大きさ」で支配法則が変わる
重力による粒子の沈降速度(落ちる速度)は、「空気抵抗」によってきまります。
ただし空気抵抗は、粒子の絶対的な大きさではなく、「 r/λ 」という、粒子半径rと空気分子の平均自由行程λ の比によって支配法則が変わります。
平均自由行程とは
気体分子は空間中を高速で飛び回っています。
空間中を移動した気体分子は、近隣の分子と衝突し跳ね返り、また空間を移動して分子と衝突し跳ね返る運動を繰り返しています。
この運動において、近隣分子と衝突してから次に別の分子と衝突するまでに移動する距離を「自由行程」と呼び、その平均値が「平均自由行程」です。
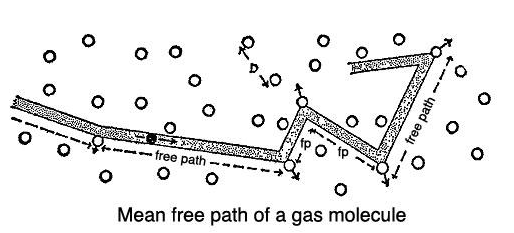
平均自由行程の長さは気体分子の熱運動で決まるので、圧力と温度に依存しますが、1気圧20℃の空気で約60nm(=0.06µm)と言われています。
粒子の大きさによって空気の「見え方」が変わる
粒子半径 r と平均自由行程 λ を比べると、いかの4つの世界に分類できます。
| 粒子の大きさ | 説明 | 支配する法則 |
|---|---|---|
| ① 分子より十分小さい(r ≪ λ) | 空気は“連続した流体”に見えない | 分子運動論の世界 |
| ② 分子と同じくらい(r ≈ λ) | 連続流体でもなく分子モデルでもない中間 | ストークス式だが補正(Cunningham補正) |
| ③ 分子より十分大きい(r ≫ λ) | 空気は“連続した流体” | ストークスの式(速度に比例) |
| ④ さらに大きい/速い | 粒子の慣性が重要 | 抗力は速度²に比例(一般的な空気抵抗) |
トナーは、「r≈4μm vs λ≈0.06μm」 なので、r は λ の約 60 倍以上になります。
つまり、トナー粒子から見た空気は 「連続体の流体」とみなせます。
トナー粒子よりさらに小さいタバコの粒子(約0.1μm)と気体分子、および自由行程を比較した図がありましたので参考までにのせます。
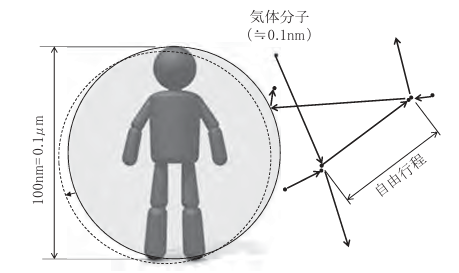
トナー粒子の話に戻すと、トナーは 「空気分子よりずっと大きい粒子」として振る舞っているといえます(空気分子から見てトナー粒子は「巨大物体」)。
空気が「連続した流体」に見えると何が起きるか?
流体の粘性が、粒子表面に「ねばり」として作用します。
- 粒子が動けば空気を引きずる
- 引きずられた空気は粒子の運動を妨げる
- この妨害力(粘性抵抗)は、ゆっくり動く粒子ほど支配的になる
この「粘性による抵抗」を数式として表したものが、 ストークスの式 です。
粘性とは
粘性とは、流体が流れるときに生じる「内部の摩擦」のことです。
水やハチミツをイメージすると分かりやすいですが、実は 空気にも粘性があります。
空気が粘性流体であるため、微小な粒子が動くと、粒子の表面の空気が「ねばり」として抵抗を生み、
その抵抗が 速度に比例 して大きくなります。
速く動くと、より強く引きずられて抵抗が大きくなる
遅く動くと、引きずりが弱いので抵抗も小さい
という性質があるのです。
空気の粘性係数は、
Wikipedia によると 1.8×10⁻⁵ Pa·s(20℃) とされています。
ストークスの式とは
粘性をもつ流体(たとえば水や空気)の中で、小さな球形の粒子がゆっくり動くとき、粒子には流体からの抵抗力(抗力)が働きます。
この「抵抗力が粒子の速度に比例する 」という関係を数式化したものが、ストークスの式(Stokesの法則) です。
F = 6 π μ r v
・Fd:抗力(粘性抵抗)
・μ:流体の粘性係数
・r:粒子の半径
・v:粒子の相対速度
つまり、粒子が速く動けば動くほど、それに比例して抵抗が大きくなるということです。
ストークスの式が成り立つ条件
ストークスの式には、いくつかの前提条件があります。
成り立つ条件
- 粒子が十分に小さいこと
- 流れがゆっくり(低速)であること(Re数が小さい)
- 粒子の形が球に近いこと
- 空気を連続した流体として扱えること(r ≫ λ)
トナー粒子は直径 5〜8 μm。
空気の平均自由行程は約 0.06 μm。
r は λ の数十倍なので、連続体として扱える条件に完全一致します。
トナー粒子でストークス抵抗を計算してみる
では実際に、トナー粒子(直径 8 μm)が空気中を動く場合の抵抗力を求めてみます。
設定値は以下の通りです。(抵抗は速度によって変わるので、ここでは終端速度で計算)
・粘性係数 :μ=1.8×10−5Pa·s(20℃の空気)
・粒子半径 :r=4×10−6 m
・相対速度:v=0.0023 m/s(=終端速度付近)
これらの数値をストークスの式に代入します。
Fd=6πμrv
Fd≈6π×(1.8×10−5)×(4×10−6)×0.0023 ≈3.1×10−12N
この値は、トナー粒子に働く 重力(約 3.2×10−12 N) とほぼ同じです。
つまり、 トナーは「重力で落ちようとする力」と「空気が引っ張り戻す力」がほぼ同じ。
そのため、ほとんど落ちず、2〜3 mm/s くらいしか沈まない、ということがわかります。
終端速度とは?
粒子は落下するとき、最初は重力で加速しますが、速度が上がるとストークス抵抗も増えていきます。
やがて、
「重力(下向き) = 抗力(上向き)」
が釣り合ったとき、加速が止まって 一定の速さ になります。
これが 終端速度(terminal velocity) です。
ストークス領域の終端速度は次で表されます。
vt=2r2(ρp−ρf)g/9μ
・トナー粒子の半径 :r = 4×10⁻⁶ m
・トナー密度 :ρₚ= 1200 kg/m³
・空気密度 : ・ρf = 1.2 kg/m³
・空気の動粘性係数 : μ = 1.8×10⁻⁵ Pa·s
・g = 9.8 m/s²
これを計算してみると、
νt≈0.0023m/s=2.3mm/s
1秒間に2.3mmずつ落下することがわかりました。
トナーはなぜ簡単に舞い上がるのか?(結論)
終端速度が たった数 mm/s しかないため、例えば装置内部の微弱な気流や、空気の揺らぎなどが 終端速度をあっさり超えてしまいます。
なので 空気が少し動けばトナーは落ちずに持ち上げられ、「浮遊トナー」として数々の問題を起こしているわけなのです。
まとめ
- トナーは空気より約1000倍重いが、
微粒子であるため 空気の粘性抵抗が重力と同じくらい強く働く - そのため落下速度(終端速度)はわずか数 mm/s
- ごく小さな気流でも簡単に舞い上がる
- 粉体工学やプリンター設計で重要になるのは「浮力」ではなく「粘性抵抗」
- この粘性抵抗を定式化したのが ストークスの式
こういった計算を実際にしてみると、単位が合っているか、という次元にも目をつけるようになり、これまでの復習にもなりました。
参考文献
・「リサイクルPETを用いたトナーバインダーの開発」三洋化成ニュース No.539
https://www.sanyo-chemical.co.jp/magazine/archives/7028
・「粗大粒子とは?クリーンルームでは対策できないって本当?粗大粒子よばれるゴミ・異物対策のプロが基本から対策方法まで解説」NCC株式会社HP
https://ncc-nice.com/ncc-clean/trivia/garbage-and-foreign-matter/sodai/
・「トナーは何からできているのですか?」リコー・サイエンスキャラバン
https://www.kouken.ricoh/science_caravan/QandA/science/qanda5_2.html
・「粒子状物質の挙動と除去機構」伊 藤 昭 三
https://www.jstage.jst.go.jp/article/jriet1972/11/9/11_9_688/_pdf/-char/ja
・「抗力係数を理解すれば空気中を移動するあらゆる物体を扱える」MONO塾
https://d-monoweb.com/blog/drag-coefficient/
・「粉体技術者のための粉体入門講座48入門の予習編-1Preparation for Lecture on Powder-1粒子の大きさについて-1」日本粉体工業技術協会
https://appie.or.jp/wp-content/uploads/2015/05/nyumon_yosyuhen.pdf
・「ストークスの法則」コトバンク
https://kotobank.jp/word/%E3%81%99%E3%81%A8%E3%83%BC%E3%81%8F%E3%81%99%E3%81%AE%E6%B3%95%E5%89%87-3156484?utm_source=chatgpt.com
・「ストークスの抵抗法則、ストークスの式」粉体工学用語辞典
https://www.sptj.jp/powderpedia/words/11122/?utm_source=chatgpt.com








コメント