前回、レーザープリンタのレーザー光の横移動速度が一定ではないと画質劣化を招く、という説明を三角関数を使って説明しました。
今回はそれを補正する役割をもつfθレンズについて学んだことをまとめます。
f-θレンズとは
その名の通り、f-θ特性をもつ光学レンズのことを指します。
このfとはレンズの焦点距離のことをいいます。
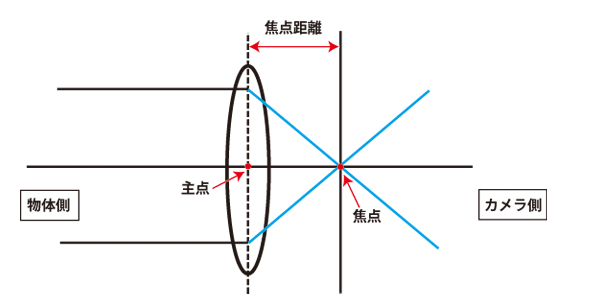
焦点距離とは、レンズの主点からレンズが像を結ぶ焦点位置までの距離の事をいいます。
・主点:主面と光軸が直交する点。
・主面:高軸に平行な光線の高さを変化させながら光学系に入射する場合に、入射前および出射後の光線をそれぞれ延長した2直線を考え、2直線の交点が描く軌跡である。
(Wikipedia参照)
これまでのレンズがない状態だと、感光体上の画像幅は、ミラーから感光体までの距離L(図ではDistance)が関係していました。
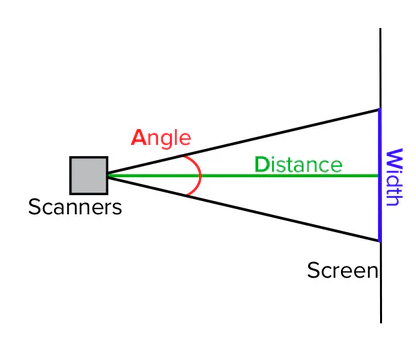
数式で表すと、
x=L×tanθ
でした。
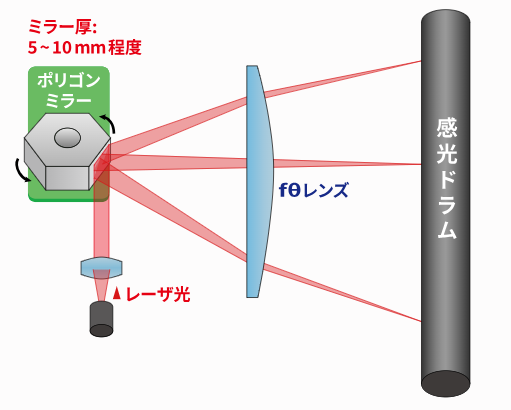
このミラーと感光体の間にレンズを置くと、画像幅(像高h)に関係してくるのはLではなく、レンズの性質(焦点距離f)が重要になります。
またこのf-θレンズは、あとで述べますが、レンズに入射してくる光の光路を曲げ、tanθの非線形の動きを線形に変える働きをするので、f-θレンズを使用した画像幅(像高h)を表す数式は、
h=f×θ
になります。
では実際にf-θレンズがどのように非線形を線形になおしているのか、難しい計算は専門家の領域なので、ここでは概念だけ理解します。
まずおさらいです。
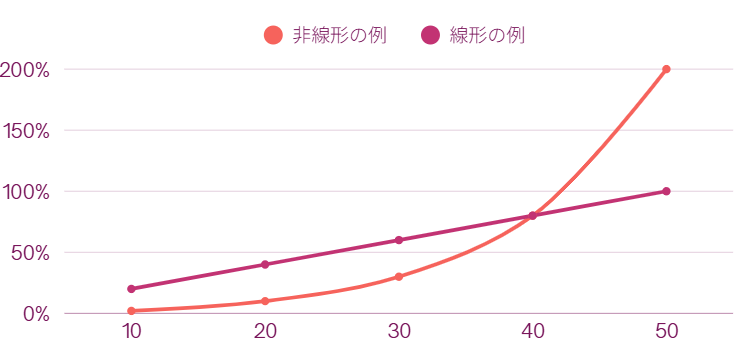
「非線形」と「線形」とは
・非線形:θが1増えたときのxの増え方が、場所によってバラバラである(グラフで表すと曲線になる)
・線形:θが1増えたときのxの増え方が、どこでも同じ(グラフだと直線)
プリンタで画質を均一なものにするためには、以下の状態にする必要があります。
「ミラー角度θが一定スピードで増え、かつ画面上の位置X一定スピードで増える」状態
= θとxが線形でつながっている状態
非線形の値
まず「非線形」の動きを具体的に数値で把握してみます。
- ミラーから感光体までの距離 L = 100 mm とする
- θ を 0°, 10°, 20°, 30° と変えてみる
1-1. tanθ を計算してみる
| θ(度) | tanθ |
| 0° | 0.000 |
| 10° | 約 0.176 |
| 20° | 約 0.364 |
| 30° | 約 0.577 |
1-2. x= L× tanθ = 100 × tanθ を計算
| θ(度) | x = 100×tanθ [mm] |
| 0° | 0.0 |
| 10° | 17.6 |
| 20° | 36.4 |
| 30° | 57.7 |
「10°ずつ角度を増やした」ときの x の増え方を見ると、
- 0°→10°:+17.6 mm
- 10°→20°:+18.8 mm
- 20°→30°:+21.3 mm
同じ10°増えてるのに、xの増え方がだんだん大きくなってるのがわかります。
これが問題の「非線形」の動きです。
線形の値
次に、理想とする線形の動きを仮に決めます。
さっきの表の 0° と 30° を通る直線を考えます。
30°のとき、x は約 57.7 mm (元の系と同じ場所を通るようにする)だとすると、1°では 57.7÷30 で約1.92mmになります。
つまり、毎角度、xが1.92mmになる動きが理想とする「線形」の動きになるということです。
補正値
ここで、元の「非線形」の曲線と「線形」の直線の動きを比較してみます。
| θ(度) | 元の像位置 x = 100tanθ | 目標像位置 x = 1.92θ | 補正値 Δx |
| 0° | 0.0 | 0.0 | 0.0 |
| 10° | 17.6 | 19.2 | +1.6 |
| 20° | 36.4 | 38.4 | +2.0 |
| 30° | 57.7 | 57.6 | -0.1 (ほぼ一致) |
※数値はざっくりです
ここで重要なのは Δx(補正値)です。
- 10°のとき:元の位置より少し横へ(+1.6 mm)補正したい
- 20°のとき:+2.0 mm 補正したい
- 30°のとき:ほぼ補正不要
言い換えると、
角度が小さい領域では、元の x が少し足りないので、もう少し幅を広げたい
30°に近くなると、元の x と直線がほぼ揃ってくる
(実際にはもっと広い角度範囲で見ると、端で「行き過ぎ」を削る方向になる場合もあります)
f-θレンズは、「欲しい位置」−「元の位置」 = Δx(θ) で出る差を、レンズ設計で位置補正しているのです。
レンズ設計については未学習の領域ですが、概念としての理解では、
様々な角度でくる光線を、レンズの曲率を変えることによって光路を理想な角度に曲げているようです。
例えば、大きい角度(走査端)からくる光線を、もっと内側に曲げるのか、逆に外側に曲げるのか。
そのために、レンズの端の曲率を強くする(よく曲げる)のか、それとも弱くする(あまり曲げない)のか…
などを 数学的に解いていって、レンズの曲面形状を決めていくのだそうです。
レーザープリンターのf-θレンズは、プリンターごとに異なる光路条件に合わせて作られているので、機種ごとに「専用設計」になります。
球面レンズと非球面レンズ
現在のf-θレンズは非球面レンズです。
非球面レンズとは、1つまたは複数の面が非球面形状を持つレンズのことです。
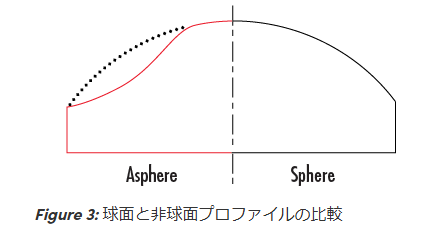
球面レンズでは屈折が単純な曲率で決まっており、角度ごとに独立した「光路調整」ができません。
一方、非球面レンズでは、端に行くほど曲率を変えてあり、中心の光線と端の光線に違う屈折を与えることができます。
この特性により、レーザープリンタ内では像高の位置補正に使用されています。
他にも、球面レンズでは球面収差というものが発生しますが、非球面レンズではこれが起きません。
球面収差とは、レンズを通過する光線が光軸上の異なる点に焦点を結び、ぼやけた像を形成する光学的効果のことです。
球面レンズでは、光軸に近い光線は屈折が少なく、レンズの端に近い光線は屈折が大きくなるため、光線の収束位置が一定に定まらないのです。
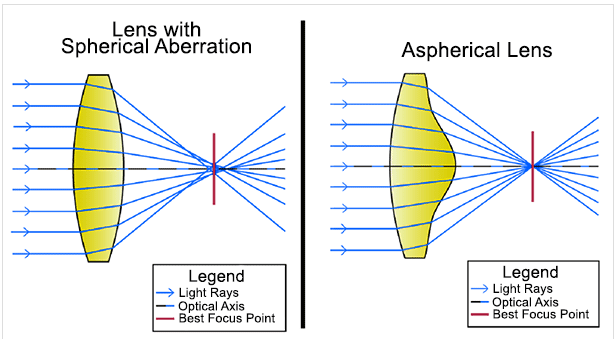
過去、これまで述べてきた「走査線のずれ」を補正すべく、様々な試行錯誤が繰り返されてきました(この歴史も深堀りすると面白そうでした)。
非球面レンズが現れるまでは、球面レンズを複数枚重ねてf-θ効果を得ていた時期もあったようですが、球面レンズゆえの問題が解消できずにいました。
現在では、主流になったこの非球面f-θレンズを「いかに小さく、薄く、歪みが少なく」「量産するか」の研究が盛んにおこなわれているようです。








コメント